多任务学习优化（Optimization in Multi-task learning）_傲世皇朝注册-傲世皇朝登录-招商中心

NEWS 傲世皇朝登录

service phone 400-123-4657

多任务学习优化（Optimization in Multi-task learning）

点击量：144 时间：2024-04-29

写在前面：多数关于多任务学习（Multi-task learning）的文章、综述或者paper都聚焦于网络结构的迭代与创新；然而，对于多任务学习Loss的优化也非常重要。本文基于多任务学习在2020年的一篇综述——《Multi-Task Learning for Dense Prediction Tasks: A Survey》中的部分内容，尽量用通俗易懂的方式来聊聊多任务学习优化的问题。

附一篇多任务学习相关文章链接《Rethink深度学习中的Attention机制》，这篇文章开篇讲述了MMoE。

以下是本文的主要框架：

A brief review
Optimization in MTL
Conclusion

全文大约6000字，阅读完大概需要15-20分钟。 PS：各位大佬不要只收藏阿，麻烦点个赞和喜欢~

大多数机器学习模型都是独立来进行学习的，即单任务学习（single-task learning）。也就是说，我们针对一个特定的任务，设计一个模型，然后进行迭代优化。对于稍复杂一点的任务，我们也习惯于通过进行拆解的方式，来对任务的每个部分进行建模。这样存在一个很明显的问题，在对每个子任务进行建模的时候，很容易忽略任务之间的关联、冲突和约束等关系，导致多个任务的整体效果无法更优。

多任务学习（multi-task learning），就是与单任务学习相对的一个概念。在多任务学习中，往往会将多个相关的任务放在一起来学习。例如在推荐系统中，排序模型同时预估候选的点击率和浏览时间。相对于单任务学习，多任务学习有以下优势：

多个任务共享一个模型，占用内存量减少；
多个任务一次前向计算得出结果，推理速度增加；
关联任务通过共享信息，相互补充，可以提升彼此的表现。

目前，多数关于多任务学习（Multi-task learning）的文章、综述或者paper都聚焦于网络结构的迭代与创新，通常会谈到软参数共享 vs 硬参数共享；或者encoder-based MTL vs decoder-based MTL；然而，对于多任务学习Loss的优化也非常重要。本文希望聊聊这个问题。

本科修经济学双学位的时候，学到过关于“零和博弈”的问题。零和博弈是博弈论的一个概念，它指的是博弈的各个参与者，在严格竞争之下，一方的收益必然会带来另一方的损失。在零和博弈下，博弈参与者们的收益和损失相加总和永远为“零”。换句话说，“损人利己”，再换句话说就是自己的幸福是建立在他人的痛苦之上。

零和博弈和多任务学习有一些共通之处。

我们以比较简单的硬参数共享的share bottom结构为例，来看看多任务学习：

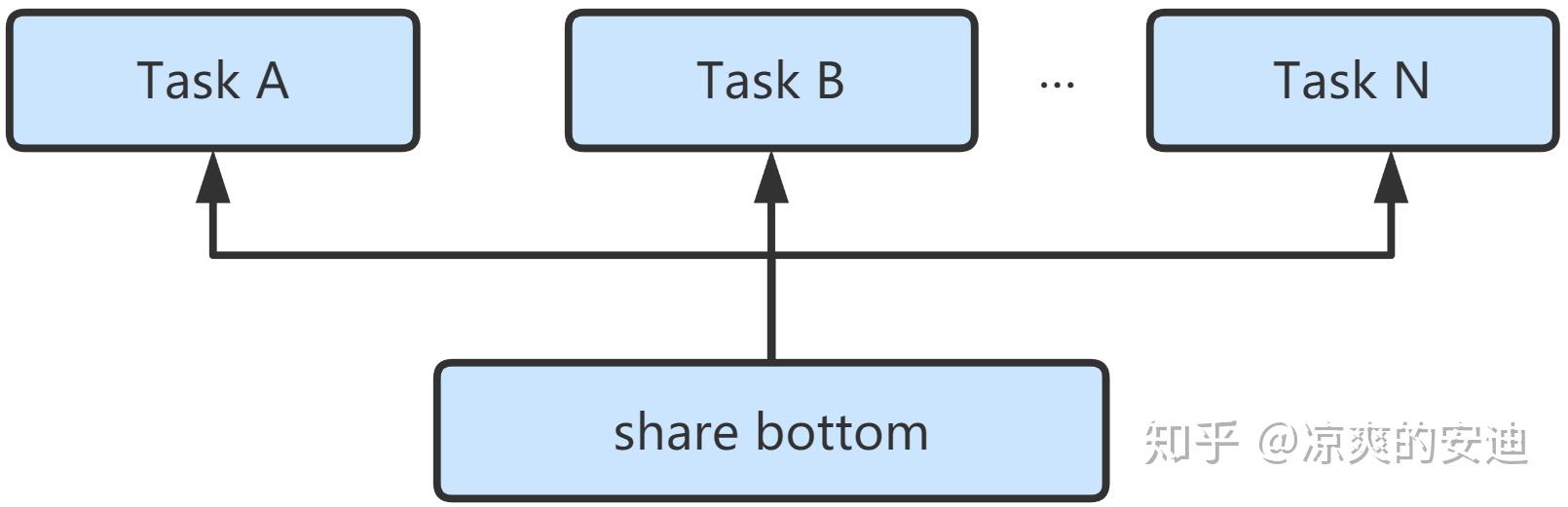
两个任务共享了input层和share bottom层，然后两个tower分别拟合两个任务的输出。对于多任务的loss，最简单的方式是直接将这两个任务的loss直接相加，得到整体的loss，那么loss函数为： $L=\\sum_{i}{L_i}$

我们发现，整体的loss来源于不同任务loss之和。

这种loss计算方式的不合理之处是显而易见的，不同任务loss的量级很有可能不一样，loss直接相加的方式有可能会导致多任务的学习被某个任务所主导或学偏。当模型倾向于去拟合某个任务时，其他任务的效果往往可能受到负面影响，效果会相对变差（这是不是有一种零和博弈的感觉，当然也有跷跷板的感觉）。

我们对loss函数进行简单的调整，对每个任务地loss配置一个固定的权重参数，那么loss函数变为：

$L=\\sum_{i}{w_i}*{L_i}$

相对于loss直接相加的方式，这个loss函数对于每个任务的loss进行加权。这种方式允许我们手动调整每个任务的重要性程度；但是固定的w会一直伴随整个训练周期。

这种loss权重的设置方式可能也是存在问题的，不同任务学习的难易程度也是不同的；且，不同任务可能处于不同的学习阶段，比如任务A接近收敛，任务B仍然没训练好等。这种固定的权重在某个阶段可能会限制了任务的学习。

那么多任务学习中，不同任务的loss的更好的加权方式是什么呢？更好的加权方式应该是动态的，根据不同任务学习的阶段，学习的难易程度，甚至是学习的效果来进行调整。（关于w的参数t的含义，我们在下文中会进行提及）

$L=\\sum_{i}{w_i}(t) *{L_i}$

接下来介绍的几个工作，主要是从不同任务loss的平衡的角度出发，动态调整不同任务loss的权重。

2-1. Gradient Normalization——梯度标准化

《Gradnorm: Gradient normalization for adaptive loss balancing in deep multitask networks》，ICML 2018，Cites：177

【主要思想】：

希望不同的任务Loss量级接近；
不同的任务以相近的速度来进行学习。

【实现】：

本文定义了两种类型的Loss：Label Loss 和 Gradient Loss。注意：这两种Loss独立优化，不进行相加。
Label Loss即多任务学习中，每个任务的真实的数据标签与网络预测标签计算的loss。Label Loss由学习任务的性质决定，比如分类的loss或者回归的loss。Label Loss通过对不同任务的Loss进行加权求和来实现： $L=\\sum_{i}{w_i}(t) *{L_i}$ 。
Gradient Loss，用来衡量每个任务的loss的权重 $w_i(t)$ 的好坏，Gradient Loss是关于权重 $w_i(t)$ 的函数。
每个任务的权重 $w_i(t)$ 是一个变量（注意这里w与网络参数W是不同的），w也通过梯度下降进行更新，t表示当前处于网络训练的第t步。

下面的几个公式是Gradient Normalization的核心，目的是将Gradient Loss表示为一个关于loss权重的函数，我们来理解一下。

首先定义了一些变量来衡量任务的loss的量级，其中：

W是整个多任务学习网络参数的子集，在文章中的实验，作者选择了网络share bottom部分最后一层的参数；
$G_{i}^{W}(t)$ 是任务i梯度标准化的值，是任务i的权重 $w_{i}(t)$ 与loss $L_{i}(t)$ 的乘积对参数W求梯度的L2范数， $G_{i}^{W}(t)$ 可以衡量某个任务loss的量级；
$\\bar{G_{W}}(t)$ 是全局梯度标准化的值（即所有任务梯度标准化值的期望值），通过所有 $G_{i}^{W}(t)$ 求均值实现。

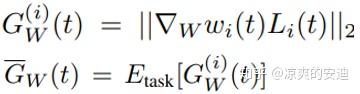
2. 其次，定义了一些变量来衡量任务的学习速度，其中：

$L_{i}(0)$ 与 $L_{i}(t)$ 分别代表子任务i的第0步和第t步的loss； $\ ilde{L_{i}}(t)$ 在一定程度上衡量了任务i的反向的训练速度， $\ ilde{L_{i}}(t)$ 越大，表示网络训练越慢；
$E_{task}[\ ilde{L_{i}}(t)]$ 表示了各个任务反向训练速度的期望；
$r_{i}(t)$ 是任务的相对反向训练速度， $r_{i}(t)$ 越大，表示任务i在所有任务中训练越慢。

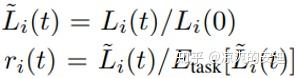
3. 最终，Gradient Loss（GL）为：

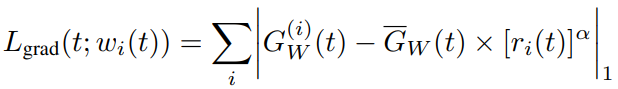
$\\bar{G_{W}}(t)$ * $r_{i}(t)$ 表示理想的梯度标准化的值；

直观来看：

$\\bar{G_{W}}(t)$ 与 $G_{i}^{W}(t)$ 用来平衡不同任务loss的量级，当某个任务loss过大或者过小的时候 $G_{i}^{W}(t)$ - $\\bar{G_{W}}(t)$ 会变大，导致loss增加；从而促使loss量级接近。
$r_{i}(t)$ 用来平衡不同任务训练的速度，当任务训练过快时， $r_{i}(t)$ 减小，使得loss增加。

计算完Gradient Loss后，通过以下函数对 $w_{i}(t)$ 进行更新(GL指Gradient Loss)：

$w_{i}(t + 1)=w_{i}(t) + \\lambda * Gradient(GL, w_{i}(t))$

GradNorm的训练流程为：

初始化各个loss的权重为1，初始化网络参数，配置 $\\alpha$ 的值，选择参数W。
通过加权求和的方式计算网络的loss。
计算梯度标准化的值 $G_{i}^{W}(t)$ ，相对反向训练速度 $r_{i}(t)$ ；
计算全局梯度标准化的值 $\\bar{G_{W}}(t)$ ;
计算Gradient Loss；
计算Gradient Loss对 $w_{i}(t)$ 求导的值；
通过第6步的结果更新 $w_{i}(t)$ ；
通过第2步的结果更新整个网络的参数；
把第7步的结果renormalize一下，使得 $w_{i}(t)$ 的和等于任务数量。

【评价】：

优点：

Gradient Normalization既考虑了loss的量级，又考虑了不同任务的训练速度。

缺点：

每一步迭代都需要额外计算梯度，当W选择的参数多的时候，会影响训练速度；
此外， $L_{i}(0)$ 过于依赖于参数的初始值；如果初始值变化很大的话，paper建议可以采用其他值代替，比如分类任务，可以用log(C) 来代替 $L_{i}(0)$ ，C是类别数量。

2-2. Dynamic Weight Averaging ——动态加权平均

《End-to-End Multi-Task Learning with Attention》，CVPR 2019，Cites：107

【主要思想】：

DWA希望各个任务以相近的速度来进行学习。

【实现】：

下面的公式是DWA的核心算法：

$w_{i}(t)$ 代表了每个任务i的权重；
$L_{n}(t-1)$ ， $r_{n}(t-1)$ 分别代表了任务n在第t-1步时的Loss和训练速度（r越小，任务训练越快）， $r_{n}(t-1) \\in (0, +\\infty)$
N代表任务的数量；
T是一个常数，T=1时，w等同于softmax的结果；T足够大时，w趋近1，各个任务的loss权重相同。

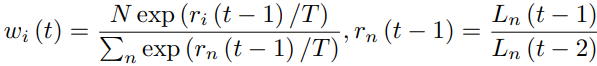
直观来看，loss缩小快的任务，则权重会变小；反之权重会变大。

【评价】：

优点：

只需要记录不同step的loss值，从而避免了为了获取不同任务的梯度，运算较快。

缺点：

没有考虑不同任务的loss的量级，需要额外的操作把各个任务的量级调整到差不多。

2-3. Dynamic Task Prioritization ——动态任务优先级

《Dynamic task prioritization for multitask learning》，ECCV 2018，Cites：53

【主要思想】：

DTP希望让更难学的任务具有更高的权重。

【实现】：

$w_{i}(t)$ 代表了每个任务i的权重；
$k_{i}(t)$ 指的是KPI，即任务i的衡量指标；KPI要选择一个衡量任务的有意义的指标，比如分类模型中的准确率等， $k_{i}(t) \\in[0, 1]$ ；KPI与任务的训练难度成反比，即KPI越高，任务越好学；
$\\gamma_{i}$ 允许为特定的任务i来调整权重；

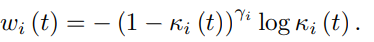
直观来看，KPI高的任务，学习起来比较简单，则权重会变小；反之，难学的任务权重会变大。

【评价】：

优点：

需要获取不同step的KPI值，从而避免了为了获取不同任务的梯度，运算较快

缺点：

DTP没有考虑不同任务的loss的量级，需要额外的操作把各个任务的量级调整到差不多；且需要经常计算KPI......

2-4. Uncertainty Weighting——不确定性加权

《Multi-task learning using uncertainty to weigh losses for scene geometry and semantics》

CVPR 2018, Cites：676

【主要思想】：

本文希望让“简单”的任务有更高的权重。

【背景】：

NIPS2017论文《What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision?》中提到，当我们使用数据集，基于输入x和输出y训练模型的时候，面临两种不确定性（Uncertainties）：认知不确定性（epistemic）和偶然不确定性（aleatoric）。

认知不确定性（epistemic）：指的是由于缺少数据导致的认知偏差。当数据很少的时候，训练数据提供的样本分布很难代表数据全局的分布，导致模型训练学偏。这种不确定性可以通过增加数据来改善。
偶然不确定性（aleatoric）：指的是由于数据本身，或者任务本身带来的认知偏差。偶然不确定性有个特点，其不会随着数据量增加而改善结果，数据即使增加，偏差仍然存在。

偶然不确定性可以分为两种情况：

数据依赖型或异方差（Data-dependent or Heteroscedastic uncertainty）。在进行数据标注的时候的误标记、错标记等，这些错误的数据也会造成模型预测偏差；
任务依赖型或同方差（Task-dependent or Homoscedastic uncertainty）。这个指的是，同一份数据，对于不同的任务可能会导致不同的偏差。比如，有个任务，我们要通过”公司 + 工作类型“来预测工作时长：

$f(t)=ax_1 + bx_2 + \\varepsilon_1$

其中，f是我们的函数，a和b是参数。“公司 + 工作类型”来预测工作时长时，本身就存在不确定性， $\\varepsilon_1$ 就是y中永远无法被x解释的部分，是一个随机变量， $\\varepsilon_1$ 就是由任务性质导致的任务依赖型不确定性；即使我们训练数据增加得再多， $\\varepsilon_1$ 仍然会存在。

而如果我们换了一个任务，我们希望通过”公司 + 工作类型“来预测所处行业，这个任务也存在误差 $\\varepsilon_2$ ，然而 $\\varepsilon_2$ 可能天然就比 $\\varepsilon_1$ 小很多。

【实现】：

回到《Multi-task learning using uncertainty …》，本文希望基于偶然不确定性（aleatoric）中的任务依赖型、同方差不确定性，来进行建模。即，对于某个样本而言，模型既预估一个标签 $f(x_{i})$ ，又预估任务依赖型同方差不确定性 $\\sigma$ 。

接下来，简单描述下loss函数的推导过程：

对于单个回归任务而言，其条件概率可以写成如下的形式，其中 $\\sigma$ 是不确定性：

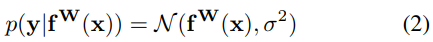
对于单个分类任务而言，模型输出一般会squash到一个softmax函数里

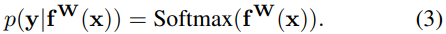
对于多任务学习而言，已知输入x， $y_{1}$ 到 $y_{K}$ 的总的条件概率可以写成预估 $y_{1}$ 到 $y_{K}$ 每一个的条件概率的乘积：

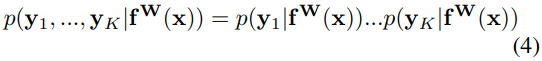
（2）式的对数似然函数正比于（5）式中右侧的部分（这一步是关键的一步，不过paper中没写推导，甚至其引用NIPS2017的paper中也没有推导。。感兴趣的小伙伴可以看看NIPS2017的paper的引用）。

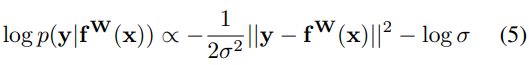
基于极大似然法对（5）式右侧的部分求极大，在神经网络里可以加一个负号求极小。

最终单个任务的loss函数为： $\\frac{1}{2\\sigma^{2}}|| y -f^{W}(x) ||^{2}+ log\\sigma$

对于多任务而言：

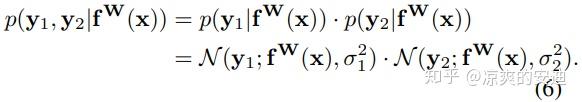
最终的loss函数为：

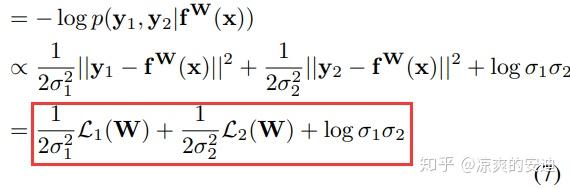
其中， $\\sigma_{1}$ 和 $\\sigma_{2}$ 是两个任务中，各自存在的不确定性。

直观来看，在一个预测任务里，如果网络可以完全overfiting到所有的样本点，那么 $|| y -f^{W}(x) ||^{2}$ 的结果应该是0，此时的神经网络变成了一个“记忆”网络，网络输出和输出之间完全变成了一种映射的关系，不确定性也自然就不存在了。

如果网络没有过于复杂，网络预测了数据的趋势，如上方举例的任务一样，但是误差 $\\sigma$ 用来衡量该任务中存在的不确定性。通过除以 $\\sigma^{2}$ ，即 $\\frac{1}{\\sigma^{2}}|| y -f^{W}(x) ||^{2}$ 的方式，可以在一定程度上对该任务带来的不确定性进行消除。而 $log\\sigma$ 则类似于一个正则项的存在，防止 $\\sigma$ 学得过大。

因此， $\\sigma^{2}$ 越大，任务的不确定性越大，则任务的权重越小，即噪声大且难学的任务权重会变小。

2-3和2-4的两个loss函数似乎存在在某种程度上是对立的。在2-3中，文章希望对于“难学”的任务给予更高的权重；而在2-4中，文章希望给“简单”的任务更高的权重。在综述中是这样写的：

We hypothesize that the two techniques do not necessarily conflict, but uncertainty weighting seems better suited when tasks have noisy labeled data, while DTP makes more sense when we have access to clean ground-truth annotations.

这两种方法不一定是完全冲突的，不确定性建模似乎可以适用于标签噪声更大的数据，而DTP可能在干净的标注数据里效果更好。（你是怎么看的呢？可以在评论区讨论一下）

3. Conclusion

本文中对于近年来几种多任务学习的loss优化方式进行了描述，主要总结如下：

重要的是，这些与优化方法与网络结构并不冲突，可以叠加产生更好的效果。快去你的多任务学习的模型里尝试一下吧 ^_^

转载前请私信！

最后的最后，求赞求收藏求关注~

参考文献

《Multi-Task Learning for Dense Prediction Tasks: A Survey》
Chen Z, Badrinarayanan V, Lee C Y, et al. Gradnorm: Gradient normalization for adaptive loss balancing in deep multitask networks[C]//International Conference on Machine Learning. PMLR, 2018: 794-803.
Liu S, Johns E, Davison A J. End-to-end multi-task learning with attention[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019: 1871-1880.
Guo M, Haque A, Huang D A, et al. Dynamic task prioritization for multitask learning[C]//Proceedings of the European Conference on Computer Vision (ECCV). 2018: 270-287.
Kendall A, Gal Y. What uncertainties do we need in bayesian deep learning for computer vision?[C]//Advances in neural information processing systems. 2017: 5574-5584.
Kendall A, Gal Y, Cipolla R. Multi-task learning using uncertainty to weigh losses for scene geometry and semantics[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2018: 7482-7491.
GradNorm：Gradient Normalization for Adaptive Loss Balancing in Deep Multitask Networks，梯度归一化
张子杨：【实验笔记】深度学习中的两种不确定性（上）

上一篇 : adam优化_耶鲁大学团队提出AdaBelief优化器，成NeurIPS 2020热点下一篇 : 有哪些免费的 AI 绘画软件分享？

返回列表